画像 y=e^-x 341876-E x p realty

Given the equation $$\left(e^{x} 1\right) y{\left(x \right)} \frac{d}{d x} y{\left(x \right)} e^{y{\left(x \right)}} = 0$$ This differential equation has the formX and Y, ie corr(X,Y) = 1 ⇐⇒ Y = aX b for some constants a and b The correlation is 0 if X and Y are independent, but a correlation of 0 does not imply that X and Y are independent 33 Conditional Expectation and Conditional Variance Throughout this section, we will assume for simplicity that X and Y are discrete random variablesSteps for Solving Linear Equation y = \frac { x y } { 1 x } y = y = 1 x x y y = Variable x cannot be equal to 1 since division by zero is not defined Multiply both sides of the equation by x1 Variable x cannot be equal to − 1 since division by zero is not defined

Differentiation Of The Exponential Function E X And Natural Logarithms Lnx Exponential Function E X Ppt Download

E x p realty

E x p realty-((y squared ) divide by 2) plus (2y(e to the power of x)) plus (y plus e to the power of x)(dy divide by dx) equally 0 ((y to the power of two) divide by two) plus (2y(e to the power of x)) plus (y plus e to the power of x)(dy divide by dx) equally zeroFor any two random variables X and Y if X Y orE X E Y E X Y E X E Y The above from MATH 3603 at HKU

If Y E Log X 5 Find D Y D X

Search the world's information, including webpages, images, videos and more Google has many special features to help you find exactly what you're looking forCharacterizations The six most common definitions of the exponential function exp(x) = e x for real x are 1 Define e x by the limit = → () 2 Define e x as the value of the infinite series = =!Take a trip into an upgraded, more organized inbox Sign in and start exploring all the free, organizational tools for your email Check out new themes, send GIFs, find every photo you've ever sent or received, and search your account faster than ever

Characteristic functions I Let X be a random variable I The characteristic function of X is de ned by ˚(t) = ˚ X(t) = EeitX I Recall that by de nition eit = cos(t) i sin(t) I Characteristic function ˚ X similar to moment generating function M X I ˚ XY = ˚ X˚ Y, just as M XY = M XM Y, if X and Y are independent I And ˚ aX(t) = ˚ X(at) just as M aX(t) = M X(at)Y x ce 2 x e x from y 0 c 1 3 hence c 2 and y x 2 e 2 y ( x ) = Ce 2 x e x From y (0) = C 1 = 3 Hence C = 2 and y ( x ) = 2 e 2 x e x Example 8 Given the IVP y 0 y = f ( x ) , y (0) = 2 , I = (0 , ∞ ) 8 where f ( x ) = 1 , 0 ≤ x ≤ 1 0 , x > 1 f is discontinuous at x = 1 From e R dx = e x , we get e x y 0 e x y = dVi vil gjerne vise deg en beskrivelse her, men området du ser på lar oss ikke gjøre det

Use the method of cylindrical shells to find the volume generated by rotating the region bounded by the given curves about the yaxis It looks as if you may have reached the right integral, which is \int_0^1 2\pi xe^ {x^2}\, dx You can quickly integrate by making the substitution u=x^2The product rule for derivatives states that given a function #f(x) = g(x)h(x)#, the derivative of the function is #f'(x) = g'(x)h(x) g(x)h'(x)# The product rule is used primarily when the function for which one desires the derivative is blatantly the product of two functions, or when the function would be more easily differentiated if looked at as the product of two functionsDepartment of Computer Science and Engineering University of Nevada, Reno Reno, NV 557 Email Qipingataolcom Website wwwcseunredu/~yanq I came to the US

The Curve Of Exponential Function Y A X A X E X If A E And X 0 Download Scientific Diagram

2

• Expectation of the sum of a random number of random variables If X = PN i=1 Xi, N is a random variable independent of Xi'sXi's have common mean µThen EX = ENµ • Example Suppose that the expected number of acci In this section we will discuss implicit differentiation Not every function can be explicitly written in terms of the independent variable, eg y = f(x) and yet we will still need to know what f'(x) is Implicit differentiation will allow us to find the derivative in these cases Knowing implicit differentiation will allow us to do one of the more important applications of derivativesX Y Z z = Z X Y Z • xyz =1 Third component can always be computed from first two • Typically, (x,y)are specified • Letαbeanypositiveconstant Then(X,Y,Z)and(αX,αY,αZ) have the same chromaticity coordinates • Projectionproperty StraightlinesinXYZ maptostraight lines in (x,y)

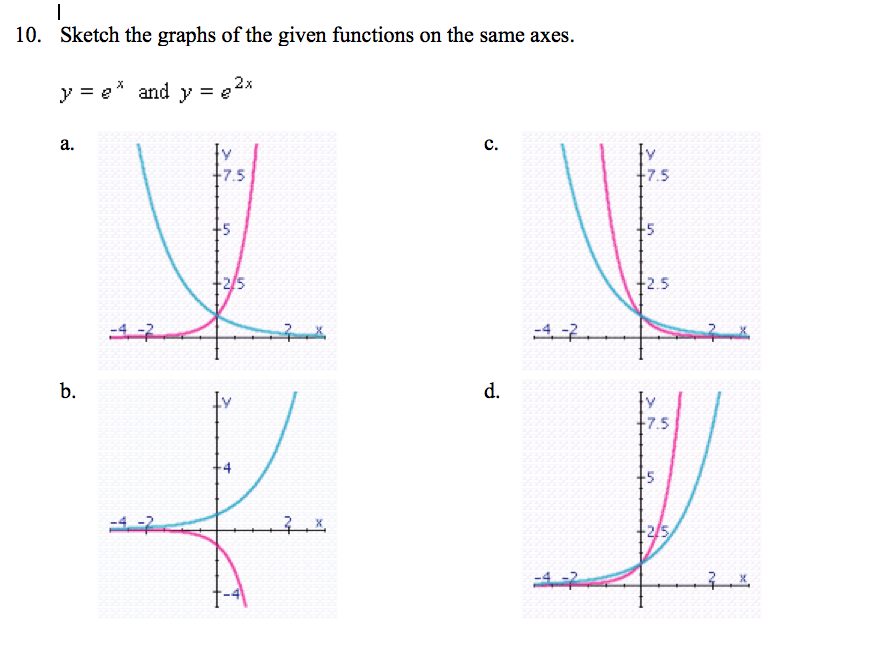
Solved Sketch The Graphs Of The Given Functions On The Same Chegg Com

Exponential

Y = a e^(b x) where a and b are constants The curve that we use to fit data sets is in this form so it is important to understand what happens when a and b are changed Recall that any number or variable when raised to the 0 power is 1 In this case if b or x is 0 then, e^0 = 1The fact that some of the coeffi­ cients are functions of x should not slow us down Applying the quadratic formula we get y = ex ± (−ex)2 − 4 1 (−ex) 2 1 ex± √ 2 4 y = 2 Our original equation isRead It Watch It Submit Answer 2 Points DETAILS SCALCET9 (a) Find the differential dy y = 24 x2 dy = (b) Evaluate dy for the given values of x Question (a) Find the differential dy y = e*/5 dy = x (b) Evaluate dy for the given values of x and dx x = 0, dx = 005 dy = = Enhanced Feedback Please try again

Y E X

Exponential And Logarithms Transformations Graphs Ppt Download

Extended Keyboard Examples Upload Random Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math1m Followers, 284 Following, Posts See Instagram photos and videos from A͙͛H͙͛N͙͛ E͙͛L͙͛L͙͛Y͙͛ (@x_xellybabyx)In addition to cookies that are strictly necessary to operate this website, we use the following types of cookies to improve your experience and our services Functional cookies to enhance your experience (eg remember settings), Performance cookies to measure the website's performance and improve your experience, Advertising/Targeting cookies, which are set by third parties with

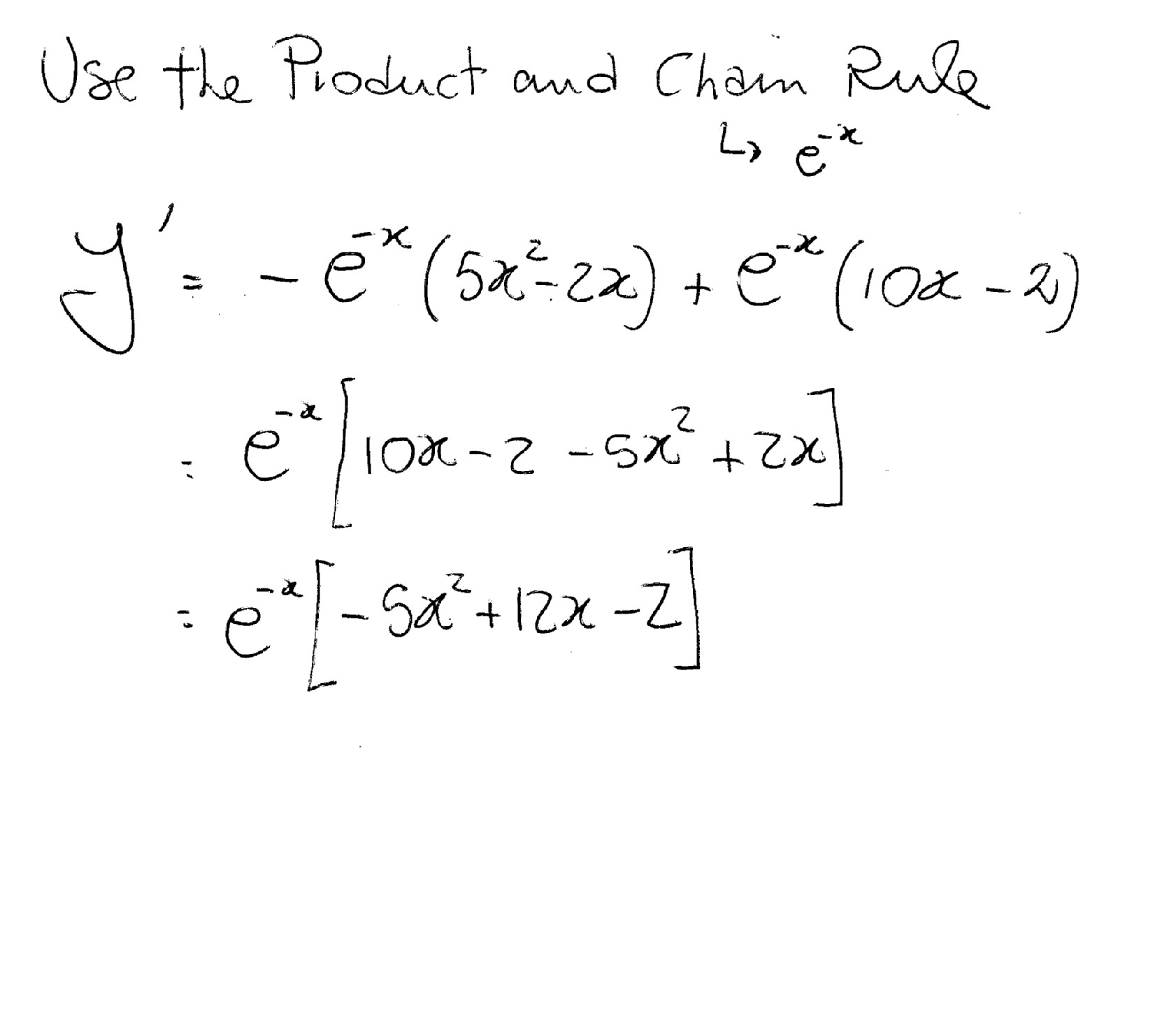
How Do You Find The Derivative Of Y E X 5x 2 2x Socratic

Resuelva Por Coeficientes Indeterminados Y Variacion De Parametros By Gerson Villa Gonzalez Issuu

Layzix (@layzix) sur TikTok 4513K j'aime 458K fans Regarde la dernière vidéos de Layzix (@layzix)Enjoy the videos and music you love, upload original content, and share it all with friends, family, and the world onY 2 − e x y − e x = 0 This is a second degree polynomial in y;

If Y E Log X 5 Find D Y D X

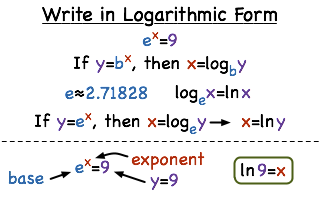
How Do You Convert From Exponential Form To Natural Logarithmic Form Printable Summary Virtual Nerd

Model Y provides maximum versatility—able to carry 7 passengers and their cargo Each second row seat folds flat independently, creating flexible storage for skis, furniture, luggage and more The liftgate opens to a low trunk floor that makes loading and unloading easy and quick Versatile seating and storage for cargo and passengersQed Example 2 edit If X {\displaystyle X} is a continuous random variable uniformly distributed on − 1 , 1 {\displaystyle 1,1} and Y = X 2 {\displaystyle Y=X^{2}} , then X {\displaystyle X} and Y {\displaystyle Y} are uncorrelated even though X {\displaystyle X} determines Y {\displaystyle Y} and a particular value of Y {\displaystyle Y} can be produced by only one or twoSOLUTION 1 Begin with x 3 y 3 = 4 Differentiate both sides of the equation, getting D ( x 3 y 3) = D ( 4 ) , D ( x 3) D ( y 3) = D ( 4 ) , (Remember to use the chain rule on D ( y 3) ) 3x 2 3y 2 y' = 0 , so that (Now solve for y' ) 3y 2 y' = 3x 2, and Click HERE to return to the list of problems SOLUTION 2 Begin with (xy) 2 = x y 1 Differentiate both sides

2

Zajecia10

X Y E olve the problem 8) A croissant, a cup of coffee, and a fruit bowl from Kelley's Coffee Cart cost a total of $525 Kelley posts a notice announcing that, effective next week, the price of a croissant will go up 25% and the price of coffee will go up 35%E(X) is the expectation value of the continuous random variable X x is the value of the continuous random variable X P(x) is the probability mass function of X Properties of expectation Linearity When a is constant and X,Y are random variables E(aX) = aE(X) E(XY) = E(X) E(Y) Constant When c is constant E(c) = c ProductY=e^ (32*x) WolframAlpha Area of a circle?

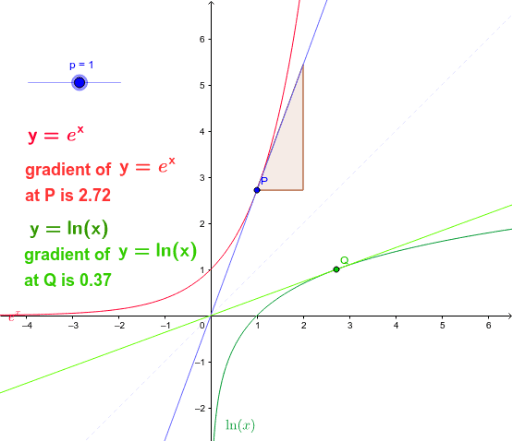
Task 4 Gradient Function Of Natural Log Geogebra

Wyznaczyc Dziedzine Zbior Wartosci I Funkcje Odwrotna Do Funkcji Y 1 2ln X 2

Note that if f(X;Y) is a linear combination of Xand Y, this result matches the wellknown result from mathematical statistics that E(aXbY) = aEXbEY = a x bIf y = ex, then ln(y) = x or If w = ln(x), then ew = x Before we go any further, let's review some properties of this function ln(x 1x 2) = ln x 1 ln x 2 ln1 = 0 ln e = 1 These can be derived from the definition of ln x as the inverse of the function ex, the definition of e, and the rules of exponents we reviewed at the start of lectureA Asus4 Well, let's steal a spaceship and head for the sun A Asus4 Shoot the stars with a lemonade ray gun F Make a movie and a TV show E You be Jane, I'm George Jetson Chorus A I am you and you are me A X, Y, Zee to A, B, Cee G A You, me, us, we are one A I am you and you are me A X, Y, Zee to A, B, Cee G A You, me, us, we are one

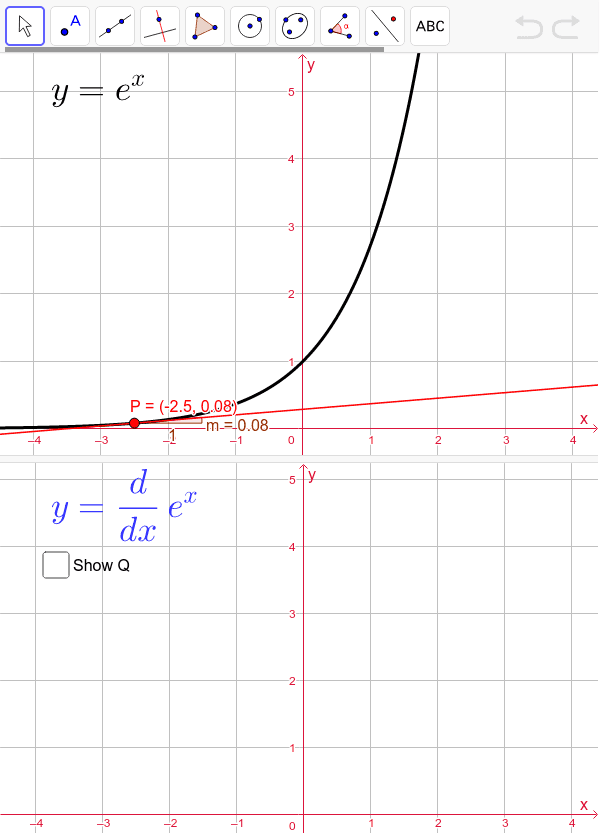
Derivative Of E X Geogebra

Lh3 Googleusercontent Com Proxy 3zp1nxzvb05viqbroiyiuehwcuzlk7zsimvze kz8p0nkzsqcxiz7xwvam Dhxuc6mvdxhlkogk9s48e4cyedxwbnu3fhhbskieeuld06bmz Qenmphenjpw4dmwnsmj14 Vpvjgk 51sx3s5rm8znnbvqgtk 9khmyeilhbbbuhq4znsnk5bhdr D0pxetqzkznsi8qqmu7ljnmpeubaizpflc3kesajup7vf3a0 Iipkzcwqki 2ff9l 791

Denotes the factorial of nOne proof that e is irrational uses a special case of this formula) 3 Define e x to be the unique number y > 0 such thatAssumeX andY bivariatenormal,asfoundbyKarlPearsonaround1900 Assume E(X)=68(inches),E(Y)=69,σ X =σ Y =2,ρ=5 (Weexpectρtobepositive becauseontheaverage,thetallerthefather,thetallertheson) GivenX=80(6feet8inches),Y isnormalwithmean µ Y ρσ Y σ X (x−µ X)=695(80−68)=75Example 5 X and Y are jointly continuous with joint pdf f(x,y) = (e−(xy) if 0 ≤ x, 0 ≤ y 0, otherwise Let Z = X/Y Find the pdf of Z The first thing we do is draw a picture of the support set (which in this case is the first

2

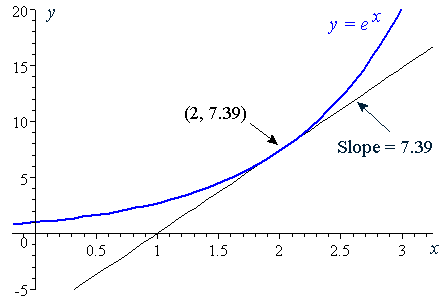
6 Derivative Of The Exponential Function

Theorem 36 Let F be any partition of the set S Define a relation on S by x R y iff there is a set in F which contains both x and y Then R is an equivalence relation and the equivalence classes of R are the sets of F Pf Since F is a partition, for each x in S there is one (and only one) set of FEasy as pi (e) Unlock StepbyStep Natural Language Math Input y The chain rule for this case is, dz dt = ∂f ∂x dx dt ∂f ∂y dy dt d z d t = ∂ f ∂ x d x d t ∂ f ∂ y d y d t So, basically what we're doing here is differentiating f f with respect to each variable in it and then multiplying each of these by the derivative of that variable with respect to t t

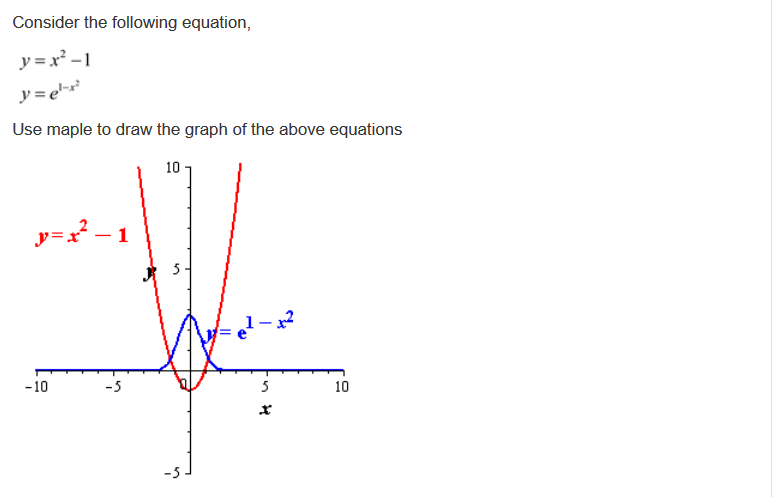
Solved How To Make Sure The Y E 1 X 2 I Just Know How To Chegg Com

Ex 5 5 15 Find Dy Dx Of Xy E X Y Class 12 Ex 5 5

Solution to Differential equations question Solve the following first order linear differential equationsy'y=(3x^24x3)e^x⃤ Plainmath is a free database8 E(X Y) = E(X) E(Y) (The expectation of a sum = the sum of the expectations This rule extends as you would expect it to when there are more than 2 random variables, eg E(X Y Z) = E(X) E(Y) E(Z)) 9 If X and Y are independent, E(XY) = E(X)E(Y) (This rule extends as you would expect it to for more than 2 randomTumblr is a place to express yourself, discover yourself, and bond over the stuff you love It's where your interests connect you with your people

Review

Differentiation Of The Exponential Function E X And Natural Logarithms Lnx Exponential Function E X Ppt Download

Okresl Punkty Przegiecia Przedzialy Wkleslosci I Wypuklosci Wykresu Funkcji Y E X X 2 4x 2 Brainly Pl

The Derivative Of E X And Lnx

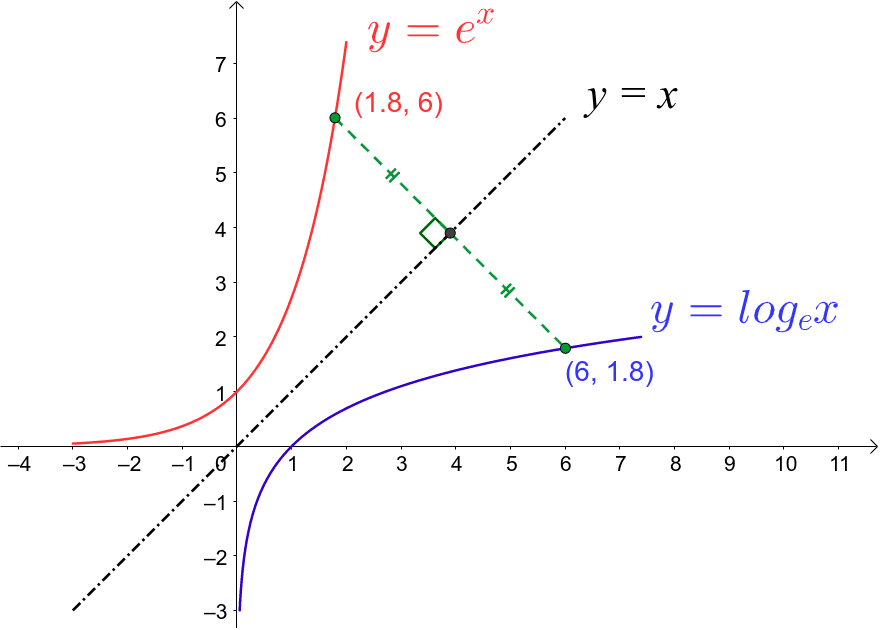
Graphs E X And Ln X Geogebra

Solved Match The Equation With The Correct Shift And Reflection Either On The Y Axis Or X Axis Y Log X 2 Y Log X 2 A Shift Horizontally Left 2 Units Then Reflect Vertically On The

Exponential Functions

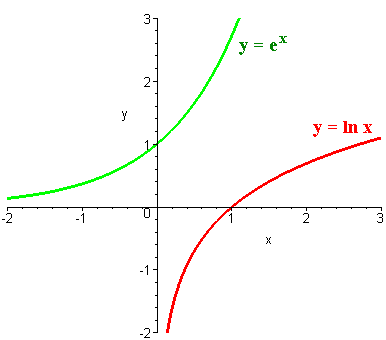
Logarithms

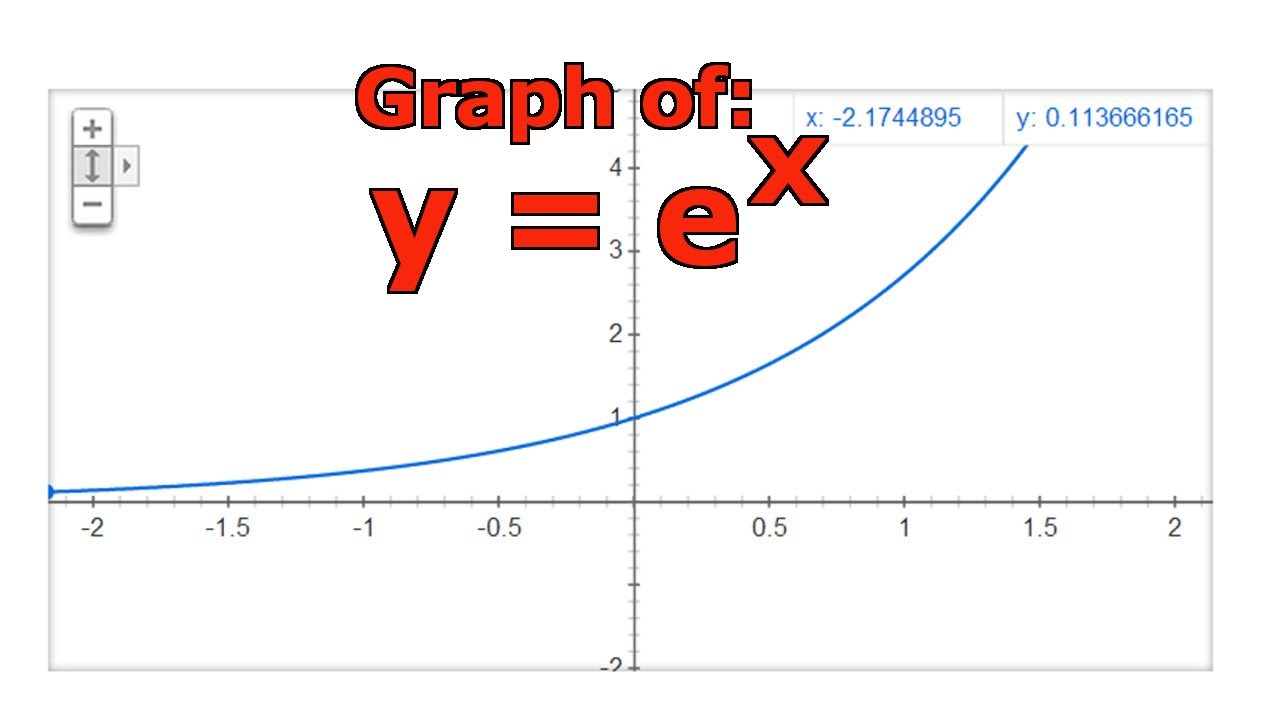
Graphing The Natural Exponential Function Y E X Youtube

Solution Y E X How Do I Graph This Please Help

Chislo E Funkciya U E X Eyo Svojstva Grafik Differencirovanie Urok Algebra 11 Klass

Differential Equation 1st Order Linear Form 8 Of 9 Example 5 Of Non Homogenous Form Youtube

Ex 9 1 8 Determine Order Degree Y Y E X Class 12

2

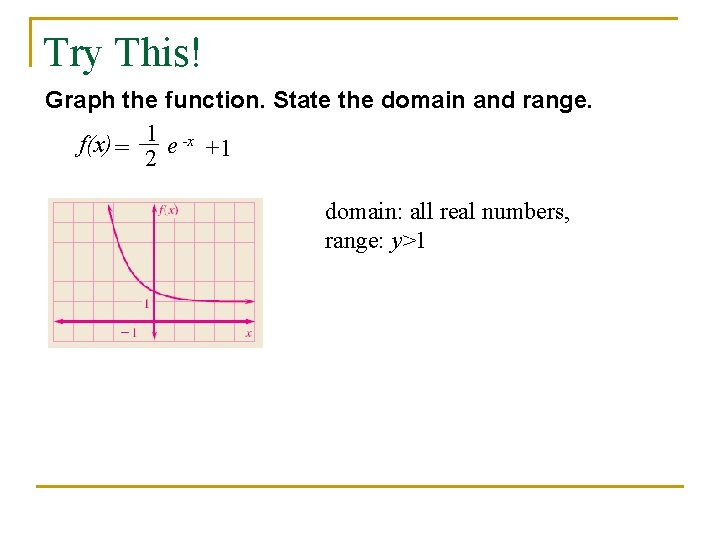
6 6 The Natural Base E Natural Base

Derivative Of 𝑒ˣ Video Khan Academy

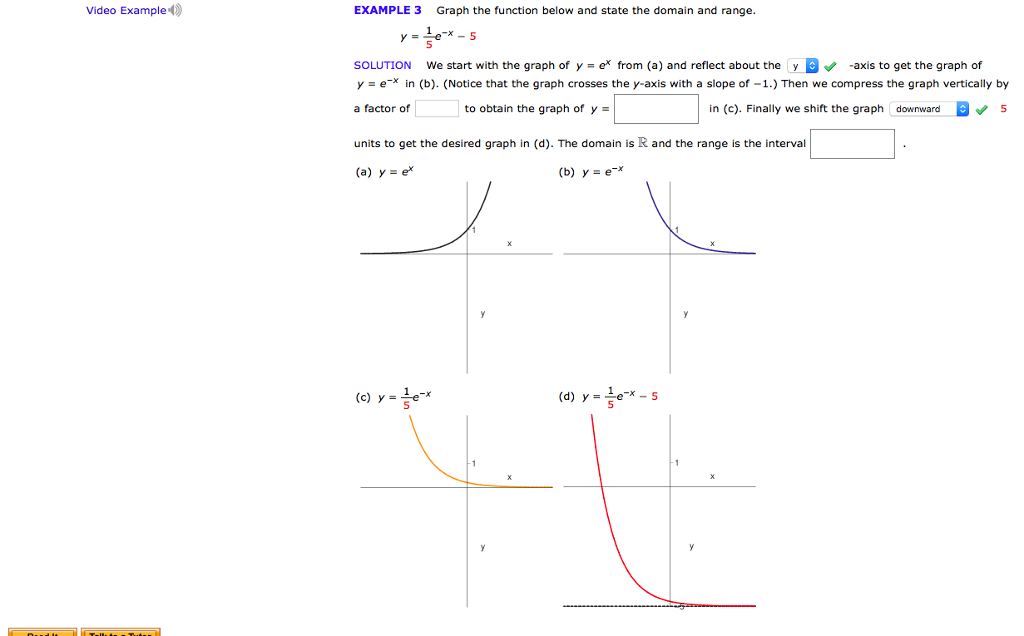
Solved Graph The Function Below And State The Domain And Chegg Com

If X Y E X Y Show That Dy Dx Logx Log Xe 2 Sarthaks Econnect Largest Online Education Community

Funkcja Wykladnicza Wikipedia Wolna Encyklopedia

Review 7 2 Find The Derivative 1 Fx

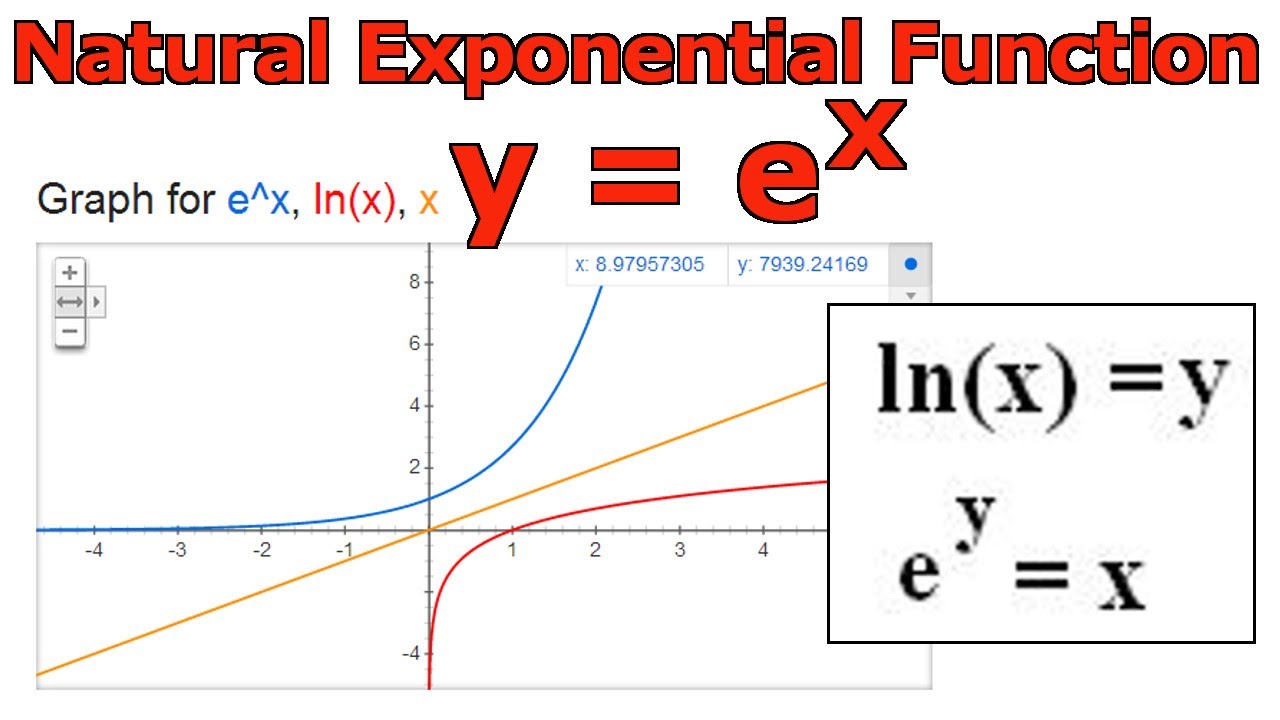
Natural Exponential Function Y E X Youtube

Exponential Functions

Yex B V Kariera I Profile Obecnych Pracownikow Znajdz Polecenia Linkedin

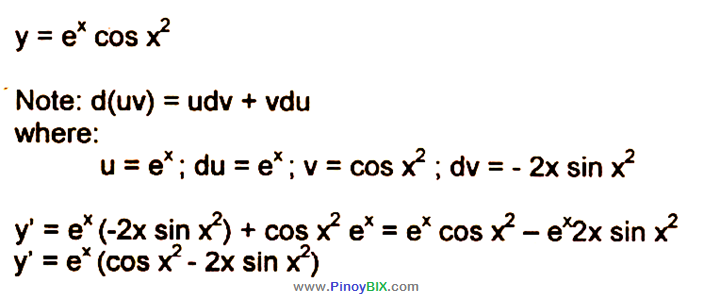
Solution Differentiate Y E X Cos X 2

Transformation Of Graphs By Modulus Function Functions Openstax Cnx

Ln Rownania I Nierownosci Procenty Matematyk Forum Matematyczne Matematyka I Fizyka

Review

Probability Covariance And Correlation Faisalkhan81 Yahoo Com

E Xy E X E Y And Pull Out Property Of Conditional Expectation Without Standard Machine Mathematics Stack Exchange

Solution Use The Graph Of Y E X To Evaluate E 1 6 To Four Decimal Places

Solve X D 2 Dx 2 2x 1 Dy Dx X 1 Y 0 Given That Y E X Is An Integral Included In The Complementary Function सम करण X D 2 Dx 2 2x 1 Dy Dx X 1 Y 0 क हल क ज ए द य गय ह क Y E X

Transforation Of Exponential Graphs Y Ex Matching Cards With Answers Teaching Resources

Graph F X To F X A Science

2

Working With Exponentials And Logarithms

Definition Of Covariance The Covariance Of X Y

General Solution Of Dy Dx E X Y Is A E X E Y C Mcq Class 12

What Are The Nth Derivatives Of Y E X Quora

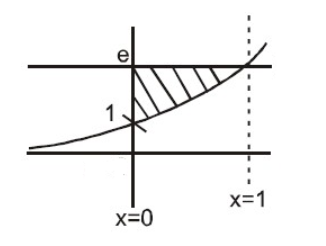
Area Bounded By Y Ex And Lines X0 And Ye Is Given By Class 12 Maths Cbse

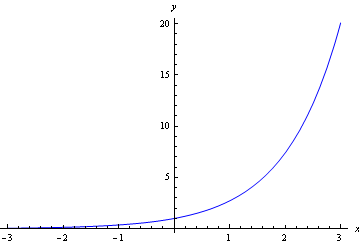
Exponential Functions

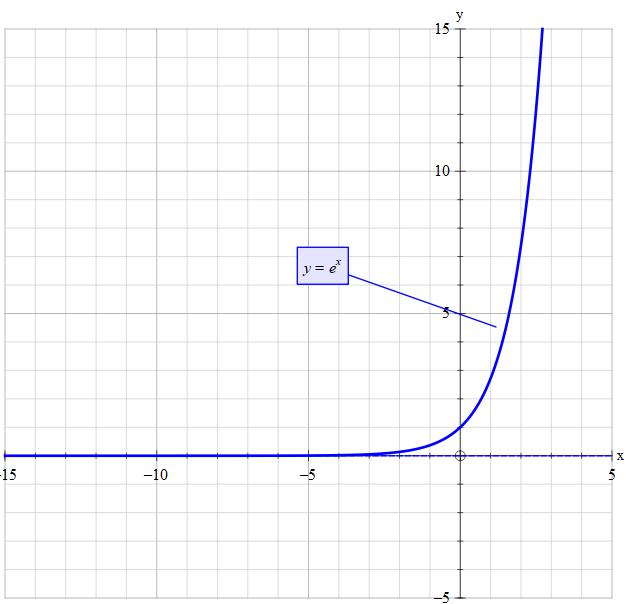
What Is The Domain And Range Of Y E X Socratic

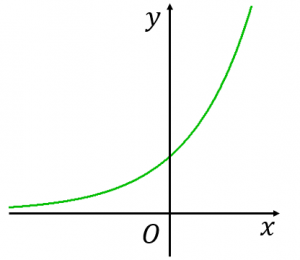
Y E Xのグラフをきれいに書く6つのコツ 具体例で学ぶ数学

E X 1 Ed E X 1

The Curve Of Exponential Function Y A X A X E X If A E And X 0 Download Scientific Diagram

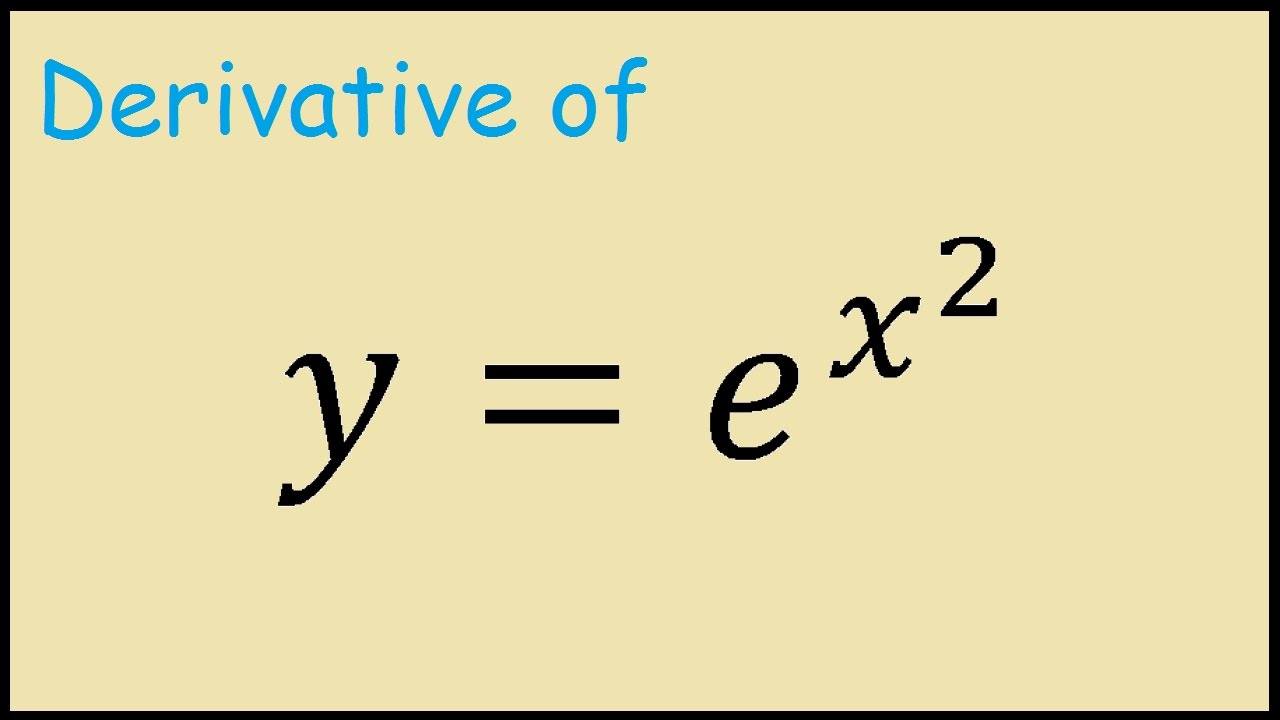
Derivative Of Y E X 2 Youtube

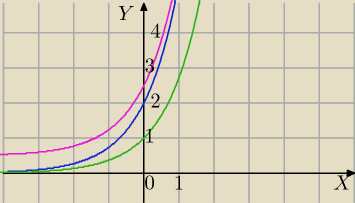
Wykres Funkcji E X Pomocy

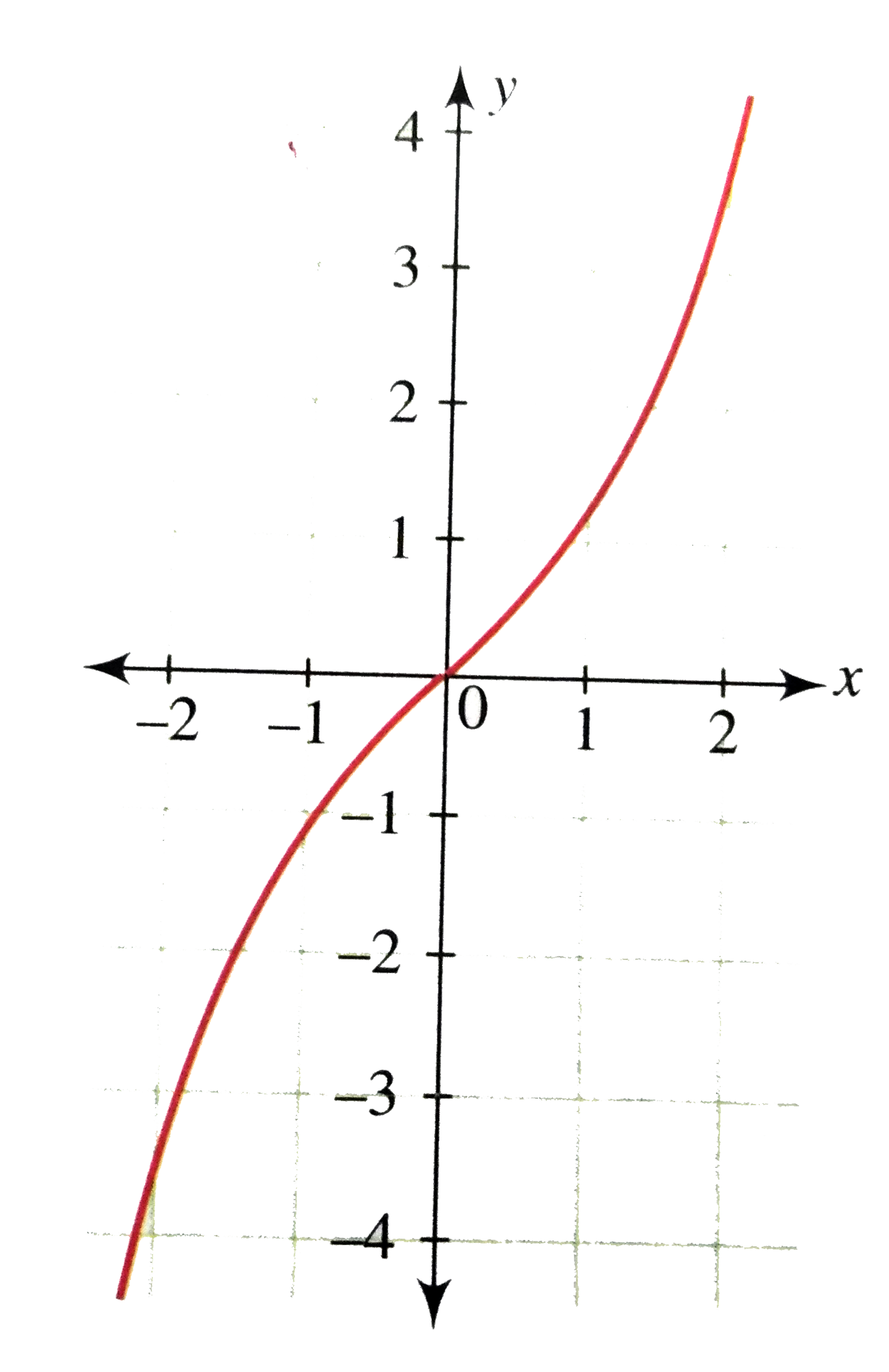
Draw The Graph Of Y E X E X 2

Solved Graph The Function Not By Plotting Points But By Chegg Com

A Sketch The Graph Of Y Ex As A Curve In R2 B Sketch The Graph Of Y Ex As A Surface In R3 C Describe And Sketch The Surface Z Ey Study Com

If Y Ex Sin X Prove That D2y Dx2 2 Dy Dx 2y 0 Explain In Great Detail Mathematics Topperlearning Com 5p09j033

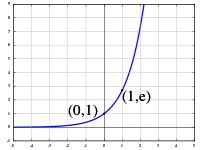
Exponential Function Wikipedia

Find The General Solution Of Y Y 2y Ex 1 Ex Stumbling Robot

Introduction We Are Going To Look At Exponential Functions We Will Learn About A New Special Number In Mathematics We Will See How This Number Can Be Ppt Download

How To Show That E E X Mid Y Mid Y E X Mid Y Mathematics Stack Exchange

2

2

Content Graphing Logarithmic Functions

Document

Solve D 3y Dx 3 3 D 2y Dx 2 3 Dy Dx Y E X 2 Mathematics 2 Question Answer Collection

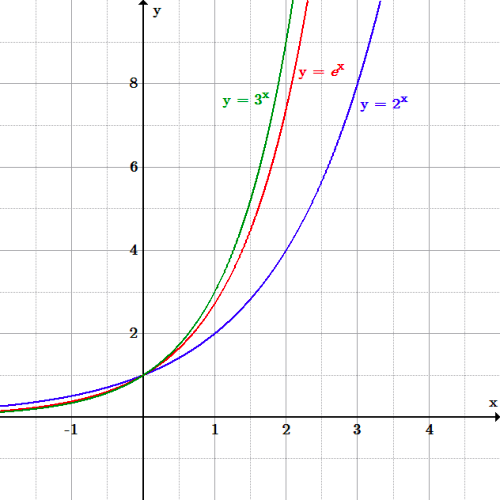
The Real Number E Boundless Algebra

The Solution Of Dy Dx Y E X Y 0 0 Is Studyrankersonline

What Is The Graph Of E X Quora

E X 0

Graphs And Level Curves

How To Sketch The Graph F X E X 1 Socratic

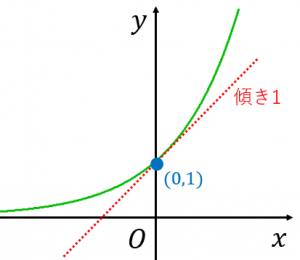
Y E Xのグラフをきれいに書く6つのコツ 具体例で学ぶ数学

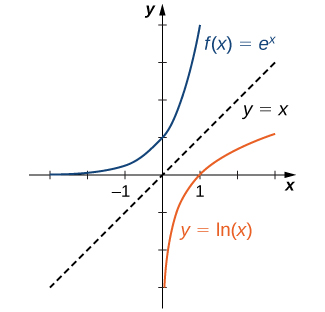
1 9 Limit Of Exponential Functions And Logarithmic Functions Mathematics Libretexts

Working With Exponentials And Logarithms

If E X E Y E X Y Prove That Dy Dx E Y X 0 Sarthaks Econnect Largest Online Education Community

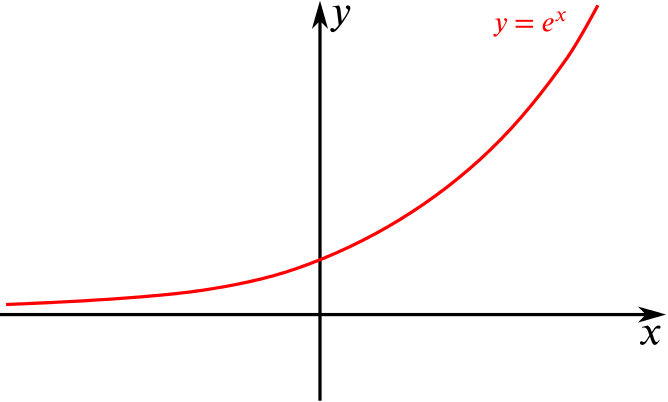
Solution Can We Sketch And Describe These Composite Functions Combining Functions Underground Mathematics

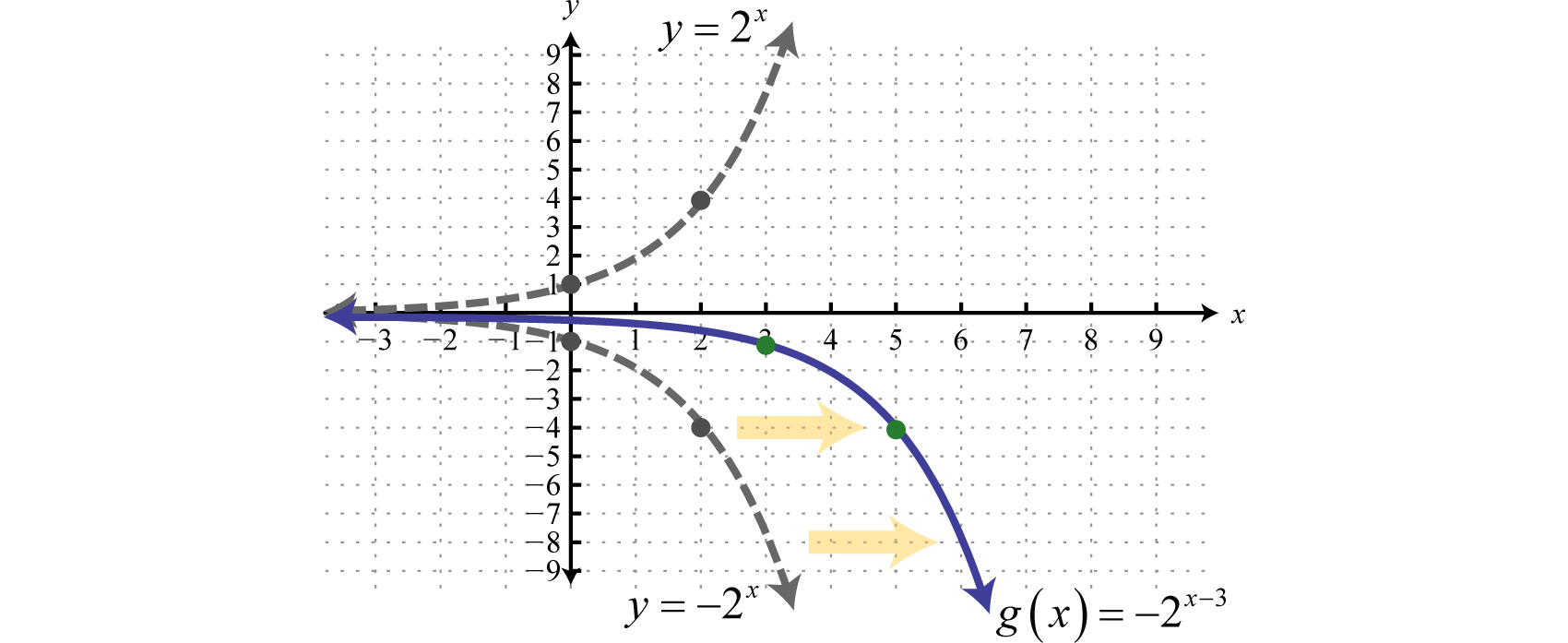
Exponential Functions And Their Graphs

Find The Area Bounded By The Curve Y E X The X Axis And The Y Axis

How To Find Dy Dx Of E X E Y E X Y Quora

If Y Ex Tan 1 X Prove That 1 X2 D2y Dx2 2 1 X X2 Dy Dx 1 X 2 Y 0 Maths Continuity And Differentiability Meritnation Com

Exponential Function Wikipedia

Exponential Functions Ck 12 Foundation

Function And Relation Library

If Y E X Cos X Show That D2y Dx2 2 E X Sinx Explain In Great Detail Mathematics Topperlearning Com Igxv9cjj

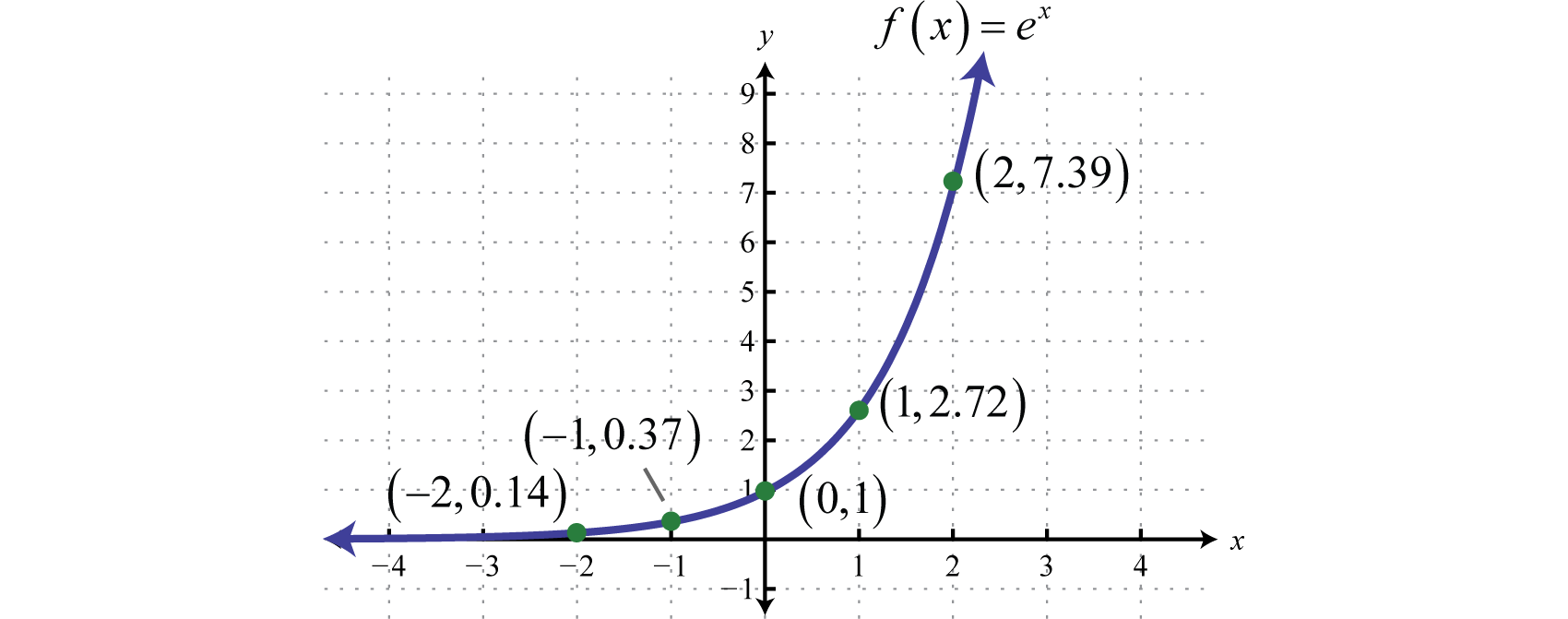
Exponential Functions And Their Graphs

If The Tangent Of The Curve Y E X At A Point C E C And The Normal To The Parabola Y 2 4x At The Point 1 2 Intersect At The Same

Incoming Term: e x graph, e x 2, e xy, e x 0, e x formula, e x taylor series, e x 1, e x^2, e x^2 formula, e x p realty,